What if Wayne Gretzky wasn’t totally right?

Welcome back, nerds. The other day, I was applying for jobs on LinkedIn — aka wandering through the emotional desert of modern job hunting. You know the drill: lots of rejection, lots of self-doubt. In one of those “should I even bother?” moments, I came across a quote you’ve probably heard a hundred times:

“You miss 100% of the shots you don’t take.”

— Wayne Gretzky

Inspiring, sure. But also… is that really true?

In sports, if you don’t take a shot, we don’t count it as a miss. And sometimes, the goals that do happen don’t even look like deliberate shots. Like the one Sidney Crosby scored on April 2, 2008, against the Flyers — a wild deflection that commentators called “completely twisted.” It didn’t look intentional, but it counted.

So I started wondering: how often do unintended goals happen? Is it possible that, sometimes, not taking a shot still ends with the puck in the net?

In this 4-part post, I’ll use PyMunk (a 2D physics engine for Python) to simulate this idea. Let’s see whether Gretzky’s quote holds up — or if, sometimes, the universe gives you a lucky bounce.

Part 1: The Premise — Gretzky’s famous quote

Part 2: What is PyMunk?

Part 3: Solving the problem.

Part 4: The results

Part 1: The Premise

“You miss 100% of the shots you don’t take.”
— Wayne Gretzky
— Also possibly his dad
— Definitely Michael Scott

It’s one of those quotes that’s so widely repeated it feels like ancient wisdom. It shows up in job interviews, sports posters, dating advice, and lottery ads. The idea is simple: doing nothing guarantees failure, while doing something — even badly — at least opens the door to success.

The first time I heard it, I was in 7th grade. My gym teacher used it to justify why he bought scratch-offs in bulk. “You won’t win if you don’t play,” he said. That version didn’t make it onto a motivational poster, but the spirit was the same.

Gretzky popularized the quote (or at least got credit for it), but similar phrases go way back. In 1943, baseball fans heard “you can’t hit the ball if you don’t swing.” In 1965, soccer had “you can’t score if you don’t shoot.” So really, Wayne just had better branding.

And yet, as I was prepping to write this article, I couldn’t stop thinking about it. Like — is it even true?

In sports, a missed shot is something measurable. If you don’t shoot, it’s not officially recorded as a miss. So technically, the quote isn’t accurate. More importantly, what about accidental goals? Can a puck bounce in off someone who wasn’t even trying to score?

That was enough to keep me up at night. And if you’ve read any of my other experiments — like 50 Cent Candy Shop Economics — you know where this is going. The only way to find out was to simulate it. Physics, code, and a million randomized hockey shots. Let’s go.

Part 2: What is PyMunk?

PyMunk is a 2D physics engine for Python, built as a wrapper around the Chipmunk C library. If that sounds like something you’d only use for side projects or indie games… well, you’re not wrong. But it’s also incredibly fun and surprisingly capable.

At its core, PyMunk lets you create little physics worlds — spaces where objects collide, bounce, roll, and occasionally score goals by accident. You define bodies (like circles or polygons), give them properties like mass or elasticity, and watch the engine simulate the chaos in real time. It’s basically a grown-up Etch-A-Sketch for kinetic nerds.

*Who Actually Uses PyMunk?
*
You won’t see PyMunk powering the backend at Google or running mission-critical infrastructure for NASA. It’s not really for that. But it is used by:

• Indie game developers building 2D physics-based games
• Educators teaching physics or simulation in Python
• Hobbyists and engineers prototyping interactions
• Artists and tinkerers who want objects to move “realistically” without hand-tuning every pixel

If you’re working in areas like simulation, ed-tech, robotics interfaces, or even interactive data viz, PyMunk can be a surprisingly intuitive way to model systems.

And yes, some weirdos use it for hockey puck probability modeling. You know who you are.

*What Problems Is PyMunk Good At Solving?
*

Anything involving 2D movement and physical interaction:

• How do two shapes bounce off each other?
• How would a box slide down a slope?
• Can I simulate a car crash with marshmallow physics?
• What happens when you shoot a puck near Gretzky 1 million times?

If you’ve ever tried to hand-code collision detection and response, PyMunk feels like cheating — in the best way. It gives you a whole engine for free, so you can focus on modeling the problem, not calculating vector math for the 47th time.

*Will It Help You Get a Job?
*

No recruiter will ever ask you, “What’s your experience with PyMunk?”
But they might want to know:

• Can you model complex systems from the ground up?
• Do you know how to simulate interactions, work with constraints, and tune parameters?
• Can you choose the right level of abstraction for the problem?

In that sense, PyMunk is a great playground for building those muscles. It’s hands-on, visual, and forces you to think in systems. Also, unlike most tutorials, there’s no login required and no five-hour install guide — just pip and play.

*Should You Learn It?
*

Only if you like fun. Or if you want to build a hockey simulator. Or if you’ve ever had a wild idea like, “What if I simulated pool balls to analyze geometry?” and didn’t want to do all the math by hand.

PyMunk won’t be on the FAANG whiteboard interview — but it might be the tool that makes you fall in love with code again. And that’s worth a shot.

Part 3: Solving the Problem

To be fair, this was my first time using PyMunk. For anyone else curious about 2D physics engines, I highly recommend giving it a try. It’s approachable enough that you can get something fun working in a few hours on a Saturday — and obsessive enough that you might find yourself simulating hockey puck deflections at 2am.

In this simulation, I modeled a half-rink in PyMunk to explore a very serious question:
What if a shot that wasn’t aimed at the goal still went in… because of Wayne Gretzky?
Could deflected shots, possibly unintentional ones, still score?

Let’s walk through how I tried to answer that — with physics, pixels, and a lot of overthinking.

*Setting Up the Rink (and the Universe)
*

In PyMunk, you define a “space” where physics takes place. Inside it, you can drop objects like circles or polygons, assign them properties (mass, velocity, elasticity), and watch them bounce around like caffeinated pinballs. It’s like CSS positioning meets mini-golf.

If you’ve ever raged at position: absolute, PyMunk will feel oddly familiar. You have:

• STATIC bodies (don’t move, like the walls)
• KINEMATIC bodies (move only if you tell them to—like the goalie and Gretzky)

• And fully dynamic bodies (like the puck, which reacts to collisions)
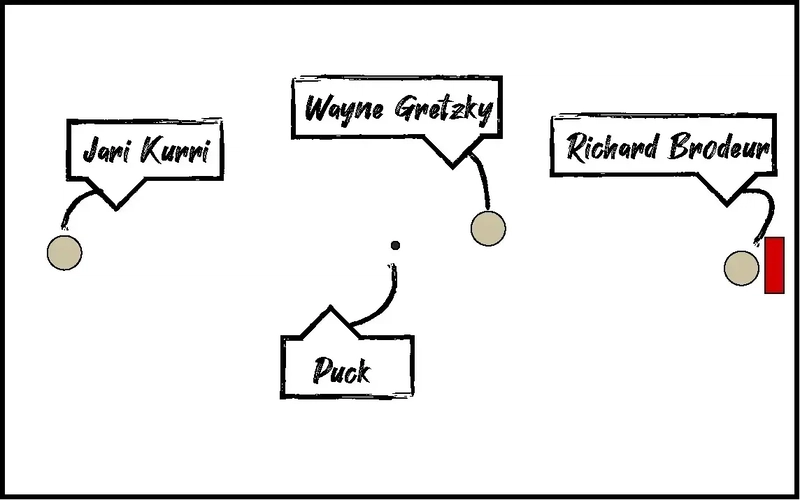
  My simulation included:

• A static rink with four walls and a goalpost

• A moving goalie (Richard Brodeur — more on that later)

• A shooter (Jari Kurri)

• A puck

• And the Beige Blur himself, Wayne Gretzky

*Scale Matters (and Shoulder Width, Apparently)
*

I wanted this to be as realistic as possible — because if you’re going to simulate deflected goals, you might as well go full NASA on the dimensions.

A standard NHL rink is 200 feet by 85 feet. I scaled it down to 1000 by 425 pixels, which works out to 1 foot = 5 pixels. That means:

• A 6-foot-wide NHL goal becomes 30 pixels wide
• A puck moves in feet per second, then pixels per second, then back to MPH for stats
• Yes, I wrote a feet_per_second_to_mph() function. Obviously.

And yes, I even looked up the average shoulder width of an adult male — 1.41667 feet, according to FreeRx.com. I scaled that up a bit for hockey pads, gear, and what we’ll generously call “off-season conditioning.”

*Shot Types and Setup Logic
*

{
  "type": "slap",
  "avg_distance": 45.02,
  "goal_pct": 2.87,
  "speedLow": 95.3,
  "speedHigh": 146.7
}

Each iteration picks a random shot and uses that to place Jari Kurri somewhere on the rink, at the correct distance from the goal. His name is no accident — Kurri had more assists to Gretzky than any other player in NHL history. If we want deflections, he’s our guy.

Here’s how Kurri gets placed:

angle = random.uniform(-0.4, 0.4)
direction = pymunk.Vec2d(-1, 0).rotated(angle)
position = goal_center + direction * avg_distance * 5

Kurri is STATIC. He’s just there to shoot, not skate.

*Enter: Wayne Gretzky
*

Wayne, on the other hand, is a moving KINEMATIC body. But placing him directly between Kurri and the goal felt wrong. The man was famous for reading the play, finding space, and creating opportunities—not just standing in the line of fire like a brave beige traffic cone.

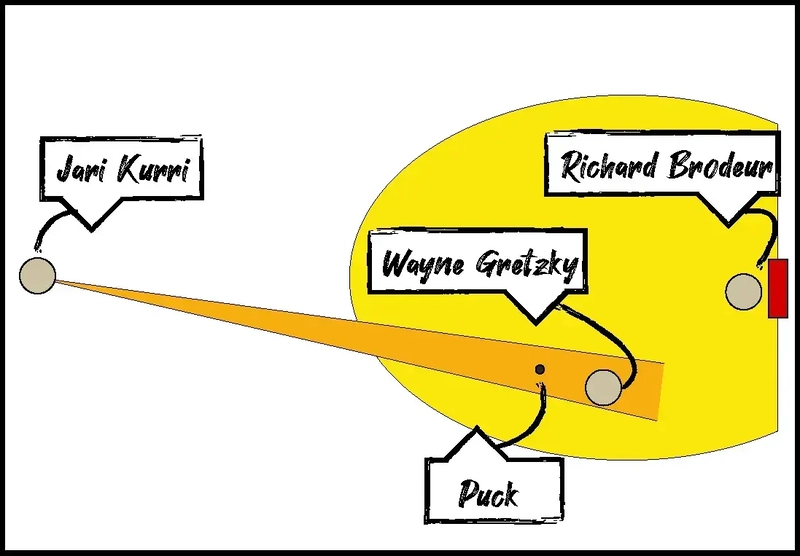
So I created a “Gretzky Zone” — an arc near the shot trajectory where he might realistically be lurking. He’s placed with some randomized angle and distance from the goal, like this:

radius = random.uniform(60, 140)
angle = base_angle + random.uniform(-0.5, 0.5)
position = goal_center + direction.rotated(angle) * radius

That puts him not too far from the path of the puck, but not predictably in the way. It’s just enough that if the puck gets a weird bounce, he might become part of the play — intentionally or not.

*The Puck and the Possibility of Chaos
*
Finally, the puck. It spawns just ahead of Kurri, aimed vaguely toward Gretzky — but not precisely. This is where the simulation gets interesting. Each shot has a bit of built-in inaccuracy, like a real human firing under pressure:

angle_variation = random.uniform(-0.1, 0.1)
aim_direction = direction_to_gretzky.rotated(angle_variation)
puck_body.velocity = aim_direction * speed_px

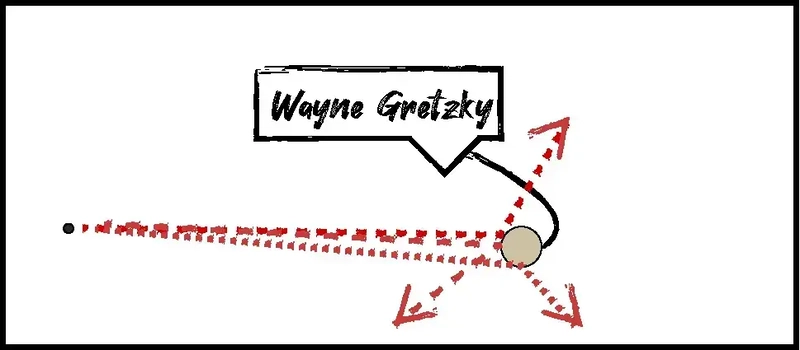
Gretzky’s movement is subtle — just a gentle drift toward the puck. The goalie (Richard Brodeur, who has the dubious honor of most goals scored against him by Gretzky) moves to track the puck in real time.

Yes, I chose Brodeur to juice the stats. This is science and comedy.

**Simulating It All
**Each simulation:

• Picks a random shot type
• Places Kurri, Gretzky, and Brodeur
• Fires the puck toward Gretzky with some noise
• Tracks collisions
• Checks if it scores, and whether Gretzky touched it
  I ran this one million times to collect enough data. I wanted to see:
  Does a shot that wasn’t “taken” by Gretzky ever go in because of him?
  We’ll find out in Part 4.

Part 4: The Results

So after one million simulated shots — yes, a full Gretzkian metric ton of physics — I finally have some results.

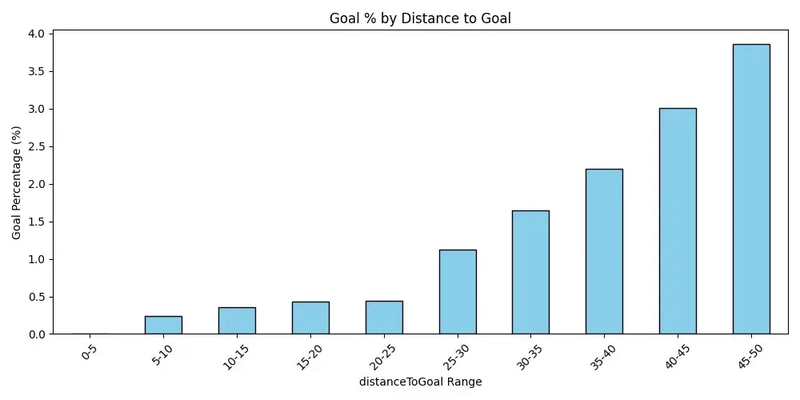
**Distance to Goal: Apparently Farther Is Better?
**Let’s start with the distance to goal. Intuitively, you’d expect tip-ins and close-range shots to dominate. You’re right in front of the net! It’s a layup, right?

Well, no. Not according to my highly scientific, mostly pixel-based simulation.

As you can see in the chart, goal percentage increased as the shot distance increased — reaching nearly 4% from 45–50 feet out. That’s longer than your average slapshot. Meanwhile, shots in the 0–20 foot range barely cracked 0.5%.

**Hypothesis:
**My guess is this has less to do with accuracy and more to do with velocity. Long-range shots have more room to build up speed, and when they do hit something — like, say, Gretzky — they’re still moving fast enough to keep going into the net. Think of it like hockey billiards: the harder you break, the more chaos you create.

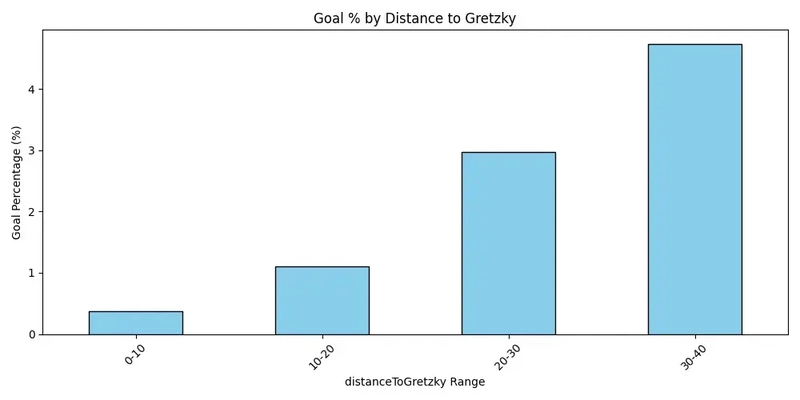
**Distance to Gretzky: The Less You Aim, The Better He Gets
**This one was fun. The simulation tracks distance between Kurri (the shooter) and Gretzky at the moment of the shot. My initial thinking: closer = better chance to deflect, right?

Nope.

As it turns out, shots with more distance between Gretzky and the shooter actually resulted in more goals off deflection. In fact, the best-performing shots had Gretzky hanging out 30–40 feet away from Kurri.

**Hypothesis:
**This lines up with the previous pattern. If Gretzky is too close, he may block or kill the puck’s momentum. Farther out, the puck’s moving fast when it hits him — causing bigger, more effective deflections. Essentially, Gretzky works better as a ricochet wall at medium-to-long range. A philosophical metaphor, maybe.

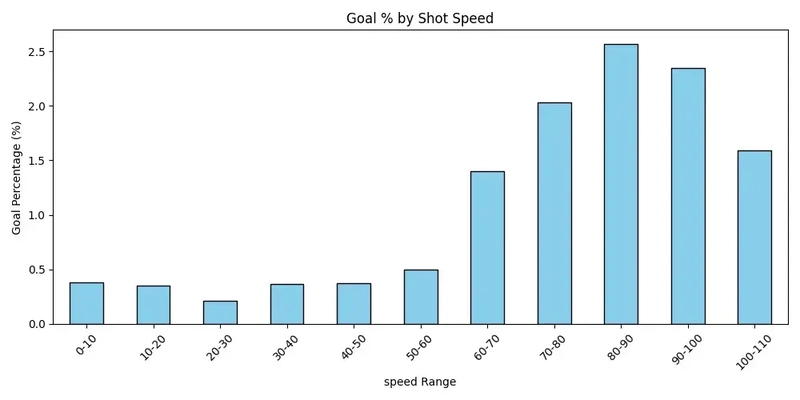
**Speed: Fast Is Good — But Not Too Fast
**Last, we looked at shot speed, measured in miles per hour. I expected a linear curve — faster shots = better chances. And we mostly got that… until it didn’t.

Goal percentage peaked in the 80–90 mph range (~2.6%) and then started to drop off at higher speeds.

Hypothesis:
There seems to be a sweet spot here. Faster shots are harder for the goalie to track, but too fast and they either miss entirely or bounce off too hard to redirect well. At ultra-high speeds, deflections become more chaotic — and harder to angle into the goal. In physics terms: there’s a diminishing return on brute force.

**The Big Number
**Across all one million simulations, only 0.057% of shots resulted in a goal off of a Gretzky deflection.

Let’s put that in perspective:

• That’s roughly 570 goals out of 1,000,000 shots
• Which is only slightly better than getting struck by lightning while buying a scratch ticket from your 7th grade gym teacher
• But still… 570 goals that wouldn’t have happened without Gretzky being there.

Conclusion

So was Gretzky right?
Maybe in spirit, but technically — no.

You don’t miss 100% of the shots you don’t take.
Because sometimes, you get a bounce. Sometimes, you’re just standing in the right place at the right time.
Sometimes… the puck hits Gretzky.